The Equation of Knowledge
There is an equation in probability theory that neatly encapsulates the ideal way to update your beliefs in the presence of evidence. It's called Bayes Theorem, and if you can bear with me for a bit, I promise this will be worth your time. I'll also make sure you can handle it even if you think you're "not a math person".
This is Bayes Theorem (odds form):
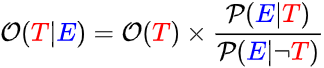
DON'T PANIC!
First off, the letters T and E that I colored red and blue stand for theory and evidence. Those aren't numbers, they're statements, such as T="The sky is blue", E="It looks blue when I look up".
The fancy letter O hugging a theory T in parentheses is the odds of your theory T. (Yes, "odds" is singular...) It's any positive number, like 10, but people often say that as "10 to 1" for reasons I'll explain in a second. You read the following as "the odds of T".

Fancy P hugging a theory T in parentheses is the probability of your theory T. It's any number between 0 and 1 (or perhaps more familiarly, any number between 0% and 100%, which is the same thing). You read the following as "the probability of T".

Odds and probability are two sides of the same coin; I'm really only introducing two different forms of one thing. The odds for a theory is equal to the probability for that theory divided by one minus the probability for that theory.

You've seen this before, when people say the odds for something are "50/50", they're saying that the probability is 50%, so the odds are 50%/(100%-50%), which is 50%/50%. If they say the odds are "80/20", they mean the probability is 80%, so the odds are 80%/(100%-80%), which is 80%/20%. Sometimes people write odds with a colon, like 80:20, but that's just another way of saying 80/20. You're also allowed to reduce this fraction, because odds of 80/20 = 8/2 = 4/1. They're all the same odds, so express it in a way that makes sense to you.
Back to Bayes Theorem. Here it is again.
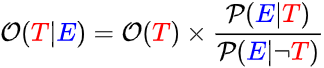
There are two other weird bits of notation in here, the vertical pipe "|" inside some of the odds and probability parentheses, and this strange symbol "¬" in the lower right.
The vertical pipe "|" inside the parentheses is read as "given", and I want you to think of it as "when we imagine we're in a universe where this other statement has been observed to be true". So the following means, "The odds of the theory T when we imagine we're in the universe where evidence E has been observed to be true":
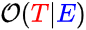
I hope this essay just got really interesting to you, because that kind of statement is something we likely really want to know every day of our lives. What are the odds of something I care about, given evidence of some kind? And there's an equals sign after it... There's an equation for that? Yes there is. No joke.
(Anyway, as an aside, when I said "imagine we're in a universe" above, I didn't mean to imply that we are not in that universe where we've observed evidence E. We might be. But we also might not be, and it's important for us to be able to leave things open until we've finished the calculation, and even after that it's important to keep an open mind, because it's easy to be fooled, either by others, or by ourselves, or by chance.)
The other strange symbol "¬" is read as "not", or "false", or "it's not true that", or "imagine we're in a universe where this thing is not true", or "imagine we have observed the absence of some evidence". The following would represent the odds that a theory T is false.
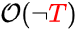
And this reads as "the probability that we would see evidence E given that we're in a universe where T is false" (which appears in the lower-right of Bayes Theorem).
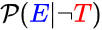
Back to Bayes Theorem again. You now have all the tools you need to understand this.
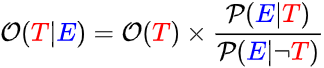
To help chunk this together in your mind, we'll label O(T) as your "prior odds", i.e., your odds for T before you saw evidence, and we'll label the division happening on the far right as a "likelihood ratio".
Bayes Theorem then simply states, "the odds of a theory T, given that we observe evidence E, is equal to our "prior odds" times the "likelihood ratio" for that evidence.
The likelihood ratio is the balance between the probabilities of seeing evidence in two different universes, one where T is true, and one where T is false (i.e., ¬T). If the probability of seeing evidence E is higher in a universe where your theory T is true than in one where it's false, your odds should go up after seeing that evidence. Otherwise, they should go down.
Pause to consider how profound it is that this equation fully captures the ideal nature of evidence and its effect on our beliefs. If you observe some evidence E, it affects your confidence in theory T in proportion to how selective that evidence is for your theory.
If that evidence pretty much only ever appears in universes where your theory is true, then seeing it is very strong evidence for your theory. The likelihood ratio is very high. If on the other hand, some evidence E is exactly as likely in universes where your theory is true as when it's false, then E doesn't change your prior odds at all. In that case the likelihood ratio is just 1, and anything multiplied by 1 is itself. Finally, if some evidence E is unlikely when your theory T is true, then seeing E is evidence against your theory. The likelihood ratio in that case is less than one, so multiplying it by your prior odds gives you a number smaller than your prior odds.
At this point, I wonder if you're wondering if you can trust this equation. I presented it as a fait accompli, and although I'm sure it seems reasonable to you in a way, perhaps you have questions. Where did it even come from? Is it merely someone's opinion, expressed as an equation? And what about all the other things that affect whether we believe something or not, such as whether we're suspicious of the source reporting the evidence to us, or how confident we were in our own prior and evidence gathering in the first place? What about the weight of authority, and what about faith?
More on these later. Let it suffice for now to say that you should try expressing each of those things in the language of Bayes Theorem, and see if you still have objections after that. The field of Probability Theory (of which Bayes Theorem is a... theorem) is all about modeling uncertainty in degrees of belief, so questions of suspicion and trust fit right in. But you can count on reading more about this later, since it's one of my primary research interests.
I'm also going to save the life lessons this equation teaches us for future posts, to keep this one lean. Stay tuned!

comments powered by Disqus